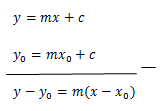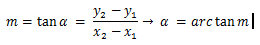2.2 PERSAMAAN NORMAL SEBUAH GARIS

B. PERSAMAAN NORMAL SEBUAH GARIS

Garis normal adalah sebuah garis yang memotong sumbu x dan sumbu y akan tegak lurus terhadap sebuah ruas garis yang melalui titik asal (0,0).

Garis OA merupakan garis normal terhadap garis l. Apabila sebuah garis m sejajar dengan sumbu x atau sumbu y, maka tidak terdapat garis normalnya.

 

Sudut 𝛽 merupakan sudut apit normal. Untuk menentukan besar sudut apit normal, kita dapat menggunakan sudut inklinasi, yaitu : 𝛽 = α – 90°. Untuk menghitung panjang garis normal, kita dapat menggunakan rumus :

Ruas garis AB adalah bagian dari garis l dan termasuk dalam kemiringan suatu garis, dimana untuk menentukan kemiringan garis (gradient) kita dapat menggunakan rumus :

m = tan α

m = tan ( 𝛽 + 90°)

α = arc tan m

Persamaan normal dari garis adalah x cos β + y sin β - p = 0

Persamaan normal dari Ax + By + C = 0

Dari persamaan normal diatas, kita dapat menyimpulkan bahwa jarak titik asal 0 ke garis lurus dengan persamaan Ax + By + C = 0 adalah

Sudut antara Dua Garis Berpotongan

Contoh 1 :

Persamaan kurva berderajat satu x + 2y - 5 = 0 pada contoh 5 dapat diubah menjadi persamaan normal dengan langkah sebagai berikut. 

1) Menentukan sudut normal 𝛽

Gradien garis yaitu 𝑚 = -1/2 maka sudut inklinasi 𝛼 = arc tan m = arc tan (-1/2) = 153,43.

Hubungan sudut inklinasi 𝛼 dan 𝛽 : 𝛼 = 90° + 𝛽. Telah diketahui sudut inklinasi 𝛼 = 153,43° maka sudut 𝛽 = 63,43°

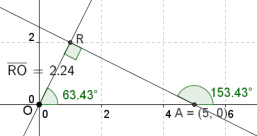
2) Menentukan jarak titik (0, 0) ke garis yaitu p

Titik potong garis dan sumbu x ditentukan dengan mensubtitusikan y = 0 sehingga diperoleh titik potong (5, 0) maka 𝑝 dibagi cos 𝛽 = 5 => p = 5 cos 𝛽 = 5 cos 63,43° = 5 . 0,447 = 2, 24

Maka persamaan normal garis x + 2y - 5 = 0 yaitu : x cos 63,43° + y sin 63,43° -2,24 = 0

Persamaan normal tersebut dapat diubah kembali menjadi persamaan garis sebagai kurva berderajat atau pun persamaan garis bergradien sebagai berikut :

x cos 63,43° + y sin 63,43° - 2,24 = 0 => 0,45x + 0,89 y - 2, 24 = 0 => x + 2y – 5 = 0

Sumber :

Catatan Kuliah , Modul Belajar

Sukirman, 1994, Geometri Analitik Bidang Dan Ruang, Jakarta : Universitas Terbuka.

Read More

2.1 KURVA BERDERAJAT SATU

A. PERSAMAAN UMUM GARIS, GRADIEN, DAN SUDUT INKLINASI 

[1.] PERSAMAAN UMUM GARIS 
         Garis dibentuk oleh paling sedikit dua buah titik berbeda. Sebagai suatu himpunan, garis merupakan himpunan titik-titik yang tak hingga dan tak berbatas sehingga garis tidak memiliki dimensi panjang. Jika garis dibentuk oleh titik A dan B maka garis tersebut dapat dinamakan sebagai garis AB. Notasi lain untuk penamaan garis yaitu menggunakan huruf kecil misalnya g, h, l, m dan sebagainya. Sebuah garis disebut kurva berderajat satu yang dinyatakan sebagai:

Ax + By + C = 0 untuk A, B, C bilangan riil dan x, y variabel bilangan riil 

Sebuah garis dapat ditentukan persamaan kurva berderajat satu seperti di atas apabila diketahui tiga buah titik yang dilalui oleh garis tersebut.

Terdapat dua persamaan garis lurus:

1.) Jika diketahui gradien garis dan sebuah titik yang dilalui garis tersebut maka persamaan garis dapat ditentukan dengan cara mensubtitusikan nilai gradien dan koordinat titik ke dalam persamaan garis bergradien m yaitu y = mx + c. Misalkan garis memiliki gradien m dan melalui titik (x₀, y₀) maka diperoleh persamaan : y₀ = m(x₀) + c selanjutnya dapat diselesaikan dengan tahapan berikut:

Persamaan yang diperoleh dinamakan persamaan garis bergradien m dan melalui sebuah titik (x₀, y₀).  Untuk dapat menggambarkan garis maka perlu ditentukan sudut inklinasi garis tersebut dengan menggunakan rumus α = arc tan m.

2.) Mengidentifikasi masalah :

Misalkan sebuah garis y = mx + c dilalui titik (x₁, y₁) dan (x₂, y₂) maka persamaan garis nya:

[2.] GRADIEN

          Kemiringan suatu garis dinamakan gradien (slope of the line) dan dinyatakan oleh notasi m. Nilai gradien suatu garis dapat bernilai positif, negatif, nol atau tidak terdefinisi. Gradien suatu garis dapat ditentukan dengan menggunakan konsep trigonometri pada segitiga siku-siku namun dengan memperhatikan interval nilai sudut yang dibentuk oleh garis terhadap sumbu x positif.

Perhatikan Gambar!

Gambar 1. Kemiringan Garis

Garis tersebut melalui dua titik yaitu P₁(x₁, y₁) dan P₂(x₂, y₂). Sudut yang dibentuk garis P₁P₂ adalah α. Pada gambar terlihat sebuah segitiga sikusiku dengan hipotenusa P₁P₂, panjang sisi alas x₂ - x₁ dan panjang sisi tegak y₂ - y₁. Nilai tangent sudut α dapat ditentukan sebagai perbandingan antara panjang sisi tegak terhadap panjang sisi alas segitiga siku-siku. Sehingga dapat dirumuskan,

[3.] SUDUT INKLINASI 

       Sudut inklinasi garis (angle of inclination) adalah sudut bernilai positif yang dibentuk antara garis dan sumbu x positif dan biasanya dinotasikan oleh sudut alpha (α).

 

Diketahui bahwa nilai gradien suatu garis merupakan nilai tangen sudut inklinasi dan besarnya sudut inklanasi adalah nilai arc tan dari gradien garis.

Perhatikan Gambar!

Gambar 2. Sudut Inklinasi (pada x positif)

dimana,

Gambar 3. Sudut Inklinasi (pada x negatif)

dimana,

 
Hubungan antara nilai gradien dan sudut inklinasi 
   adalah nilai gradien pada suatu garis merupakan nilai tangent sudut inklinasi dan besarnya sudut inklinasi adalah nilai arc tan dari gradient garis. Bentuk dari persamaan kurva berderajat satu dapat diubah menjadi fungsi dari x dimana x adalah variable bebas dan y adalah variable terikat yaitu sebagai berikut :

Konstanta m disebut sebagai gradien yang menunjukkan kemiringan garis dan c merupakan konstanta persamaan. Persamaan y = mx + c disebut persamaan garis bergradien m.

Sifat-Sifat Garis Dalam Bidang : Kesejajaran dan Perpotongan

Sifat-sifat garis yang berada dalam sebuah bidang dalam geometri Euclide meliputi garis-garis yang berpotongan atau tidak berpotongan. Dua buah garis dikatakan berpotongan jika ada sebuah titik potong yang dilalui kedua garis. Dua garis tidak saling berpotongan disebut garis sejajar. Perhatikan bentuk garis-garis pada gambar dibawah ini.

Gambar di atas memperlihatkan bahwa garis-garis bergradien positif atau negatif memotong sumbu x dan sumbu y masing-masing di satu titik. Perpotongan garis tersebut dengan sumbu x ditentukan dengan mensubstitusikan nilai y = 0 ke dalam persamaan garis. Perpotongan garis tersebut dengan sumbu y ditentukan dengan cara mensubstitusikan nilai x=0 ke dalam persamaangaris. Sedangkan garis sejajar sumbu x hanya memotong sumbu y dan tidak memotong sumbu x. Garis sejajar sumbu y hanya memotong sumbu x dan tidak memotong sumbu y. Tabel berikut meringkas hubungan persamaan garis dan titik-titik potong garis terhadap sumbu x dan sumbu y.

Persamaan-persamaan garis:

Sumber :

Catatan Kuliah , Modul Belajar

Sukirman, 1994, Geometri Analitik Bidang Dan Ruang, Jakarta : Universitas Terbuka.

Read More